Algorithms

The Token Bucket (or Leaking Bucket) algorithm is a mechanism to rate-limit the average traffic in a stream, while allowing for a certain amount of burstiness as well.

Every once in a while, I need to evaluate the normal distribution function $\Phi(x)$:

$$ \Phi(x) = \frac{1}{\sqrt{2 \pi}} \int_{-\infty}^x \! e^{-\frac{1}{2}t^2} \, dt $$

Unfortunately, it is not always available in the standard math libraries, and hence I have to implement a “good-enough” version myself. Here are some options.

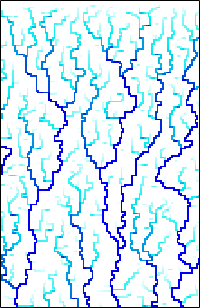
A while back, I looked at the Diamond-Square Algorithm for terrain generation. That is a purely procedural algorithm that only attempts to generate realistic looking landscapes, without trying to model any physical or geological processes. By contrast, we will now look at an algorithm to generate realistic river networks, which is based on a (simplified) model of geological erosion.

How short can a complete, competitive sort algorithm be? Less than half a dozen lines? Maybe just 3 or 4?

Selecting a random element from an array of length n is easy: simply generate a random integer i, with 0 <= i < n, and use the array element at that index position. But what if the length of the array is not known beforehand, or is, in fact, infinite (i.e. a stream)? And what if we don’t just want a single element, but a set of m samples, without replacement?

Shuffling a collection of items is a surprisingly frequent task in programming: essentially, it comes up whenever a known input must be processed in random order. What is more, there is a delightful, three-line algorithm to accomplish this task correctly, in-place, and in optimal time. Unfortunately, this simple three-line solution seems to be insufficiently known, leading to various, less-than-optimal ad-hoc alternatives being used in practice — but that is entirely unnecessary!

The Nelder-Mead-Algorithm (also known as the “Simplex Algorithm” or even as the “Amoeba Algorithm”) is an algorithm for the minimization of non-linear functions in several variables. In contrast to other non-linear minimization methods, it does not require gradient information. This makes it less efficient, but also less prone to divergence problems. In contrast to other methods, it is not necessary for the minimum to be bracketed by the initial guess: the algorithm performs a limited “global” search. (It may still converge to a local, rather than the global extremum, of course.) Finally, the algorithm is fairly simple to implement as a stand-alone routine, which makes it a natural choice for multi-dimensional minimization if function evaluations are not prohibitively expensive.

Imagine a shared resource, such as a compute server. Users can submit jobs to the server. The resource is “free”, in the sense that no costs are imposed on the users. The question is how to best assign and prioritize jobs when multiple users submit jobs simultaneously.

Finding a realistic (or at least, realistic looking) initial configuration of game objects or simulation particles can be a challenge. The desired configuration should appear to be both “random” and at the same time “spatially uniform”, without objects clustering together or overlapping.

I have started to get interested in Hidden Markov Models (HMM). As a warm-up, I prepared a pure Python implementation of the relevant algorithms (github).